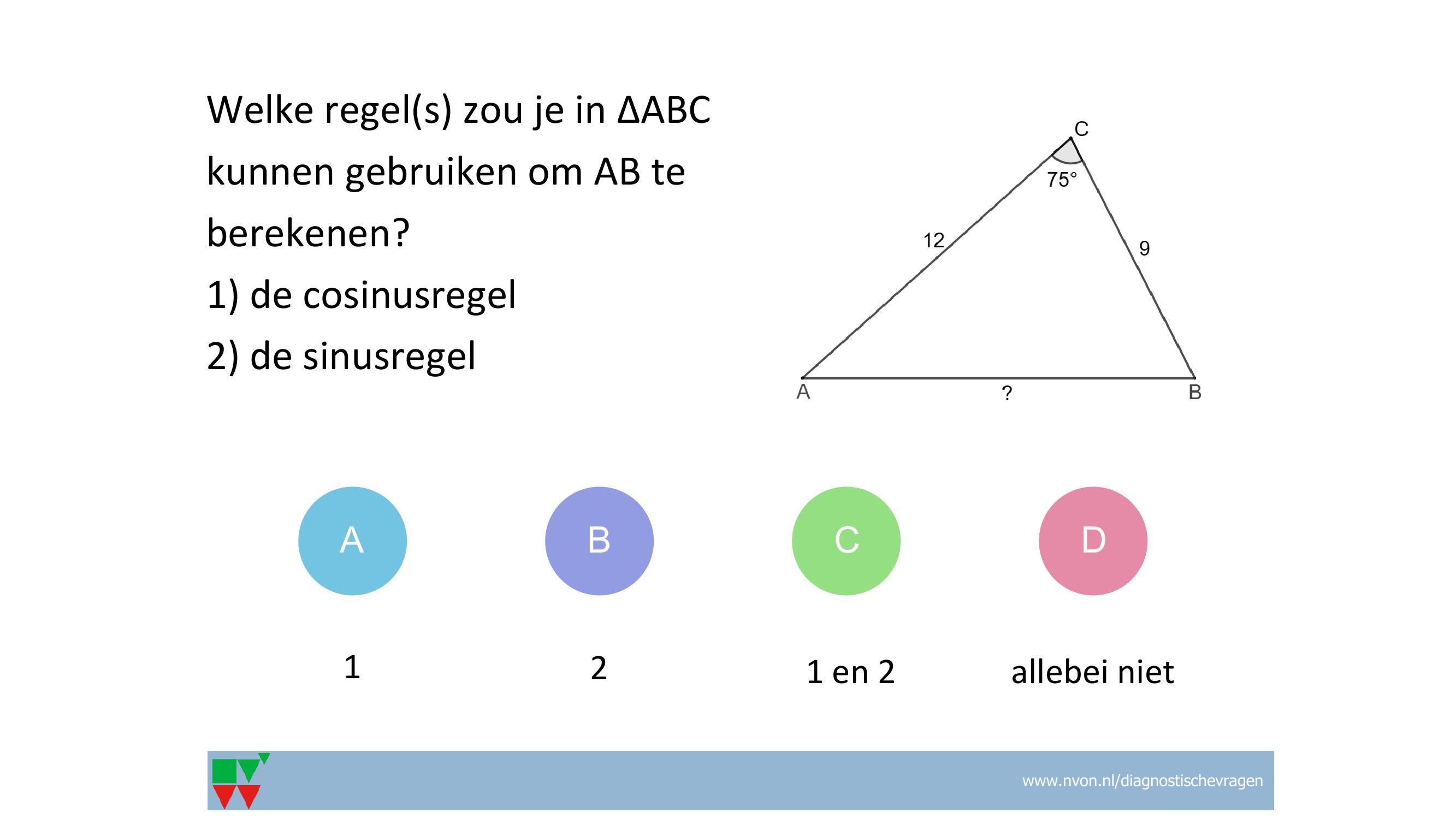
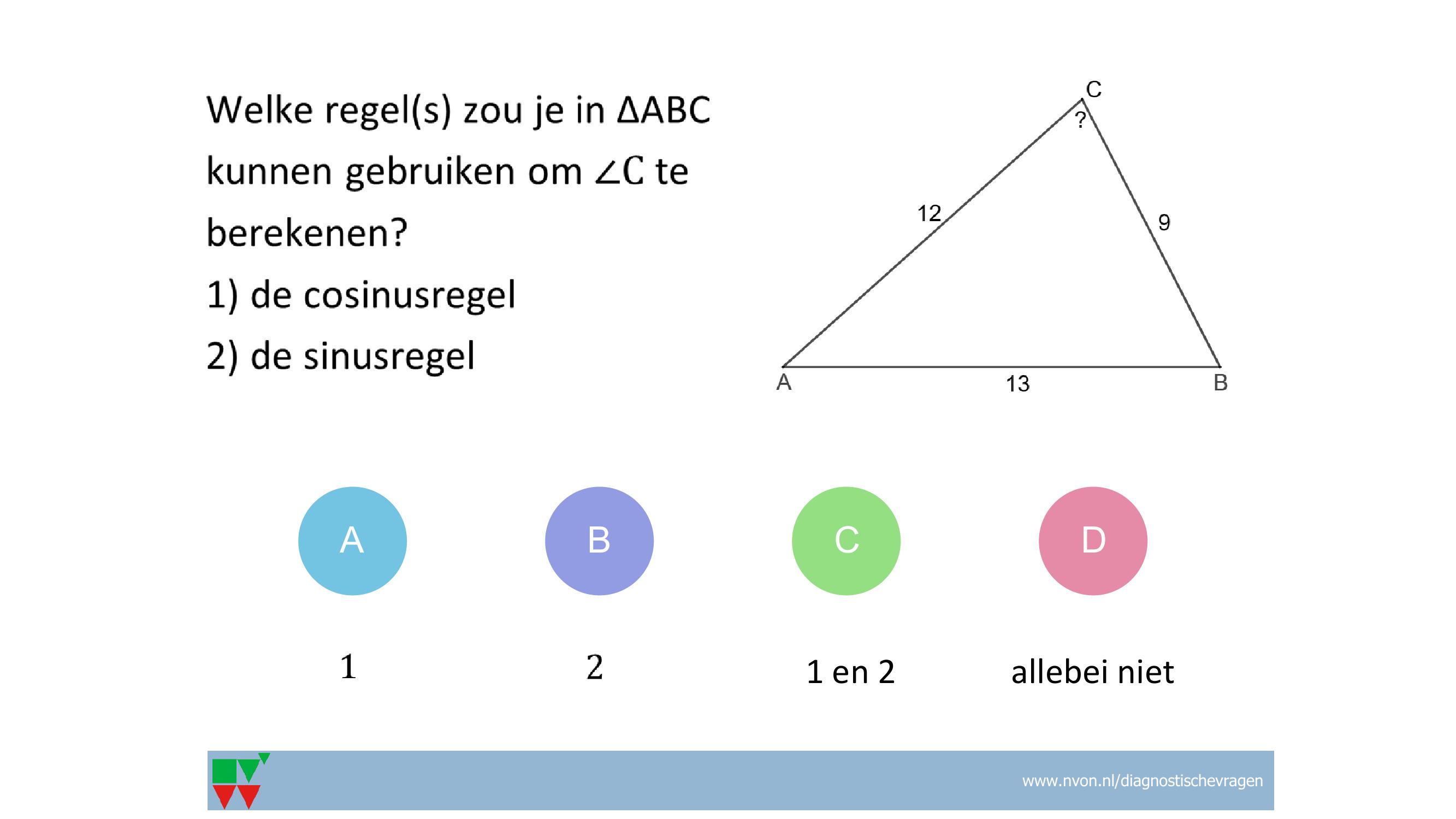
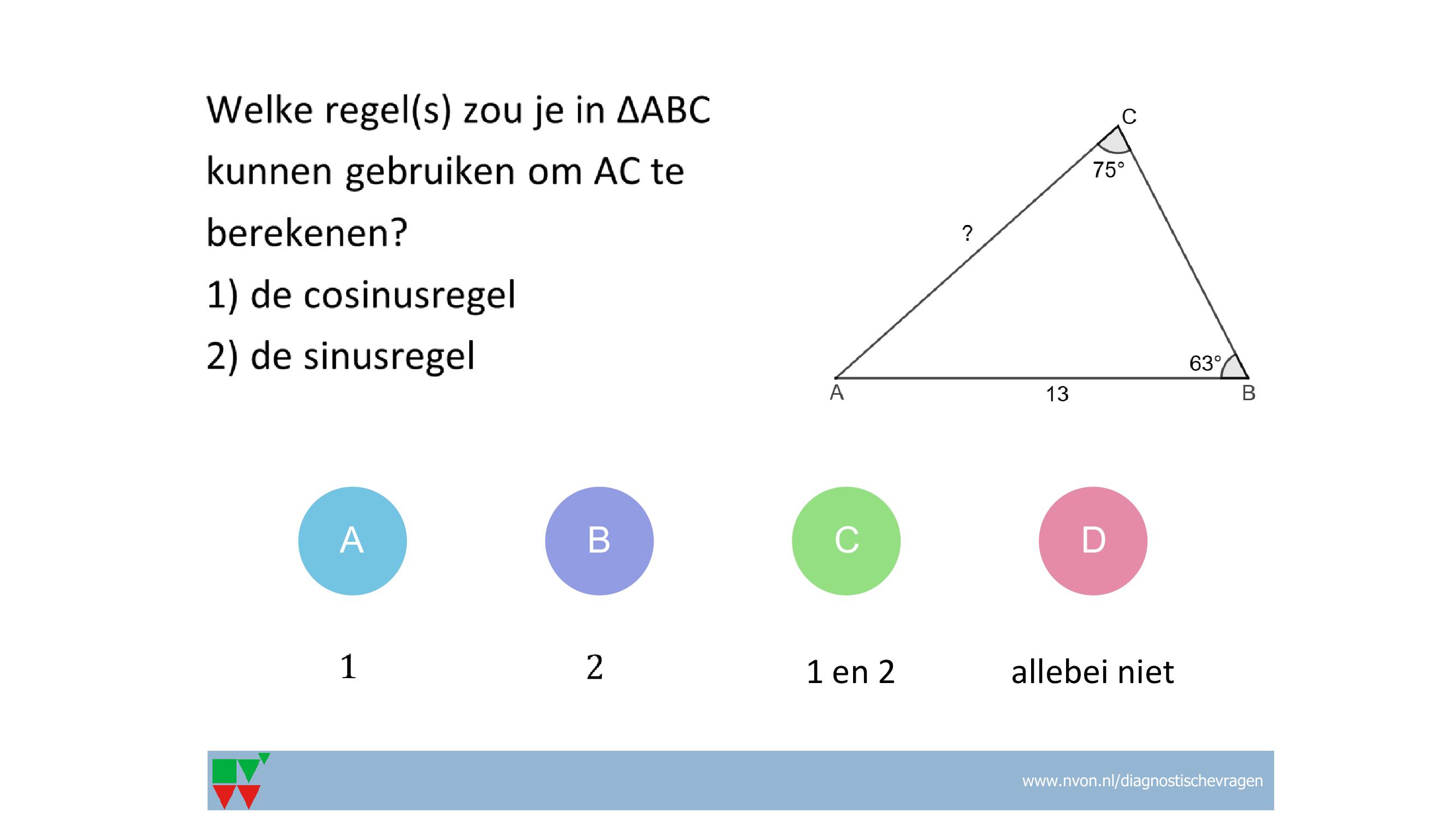
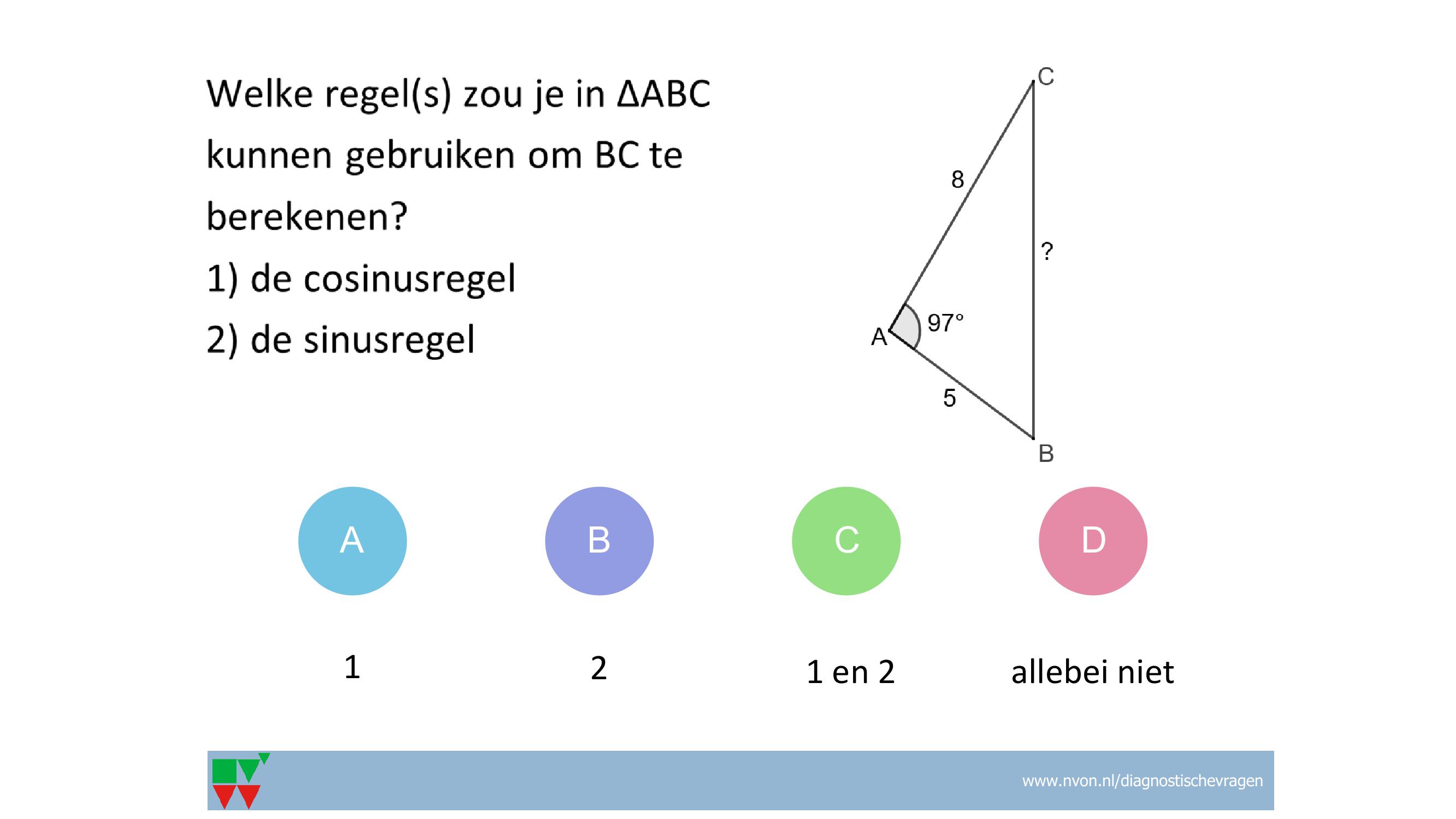
Verbanden en formules Lineair verband, formules opstellen
Wiskunde voor niveau havo 4, havo, vwo, havo 3, vwo 3, vwo 4, vwo, 3, vwo, 4
PowerPoint met diagnostische vragen over formules opstellen bij een lineair verband.
lineair verband, formule, formule opstellen, richtingscoefficient, lijnstuk, lijn, iol
Hieronder zie je de dia’s inclusief toelichting. Gebruik de knop hieronder om de presentatie (Powerpoint) te downloaden.
Download presentatie (.pptx)
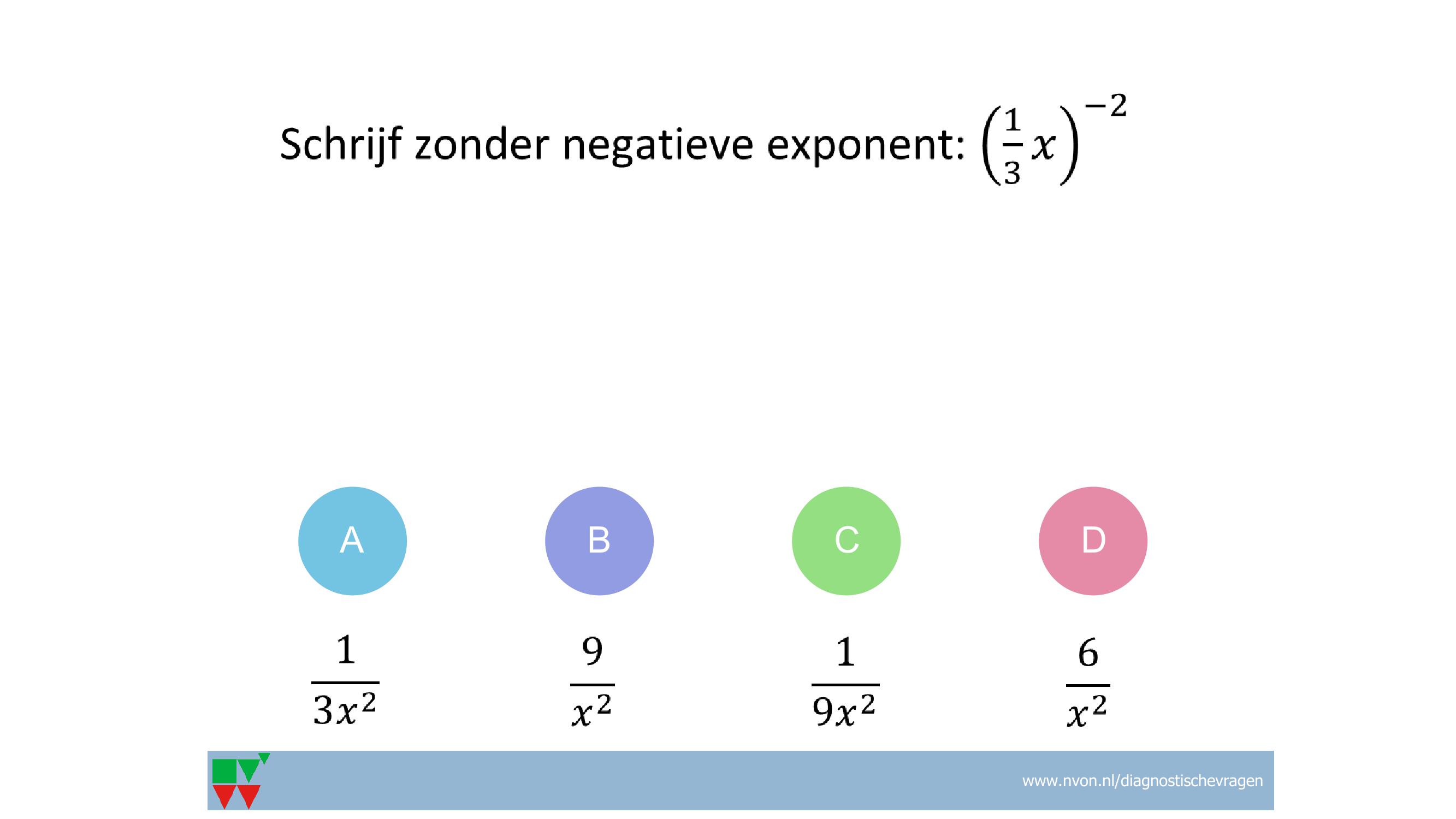
VF-48
Misvatting: Bij de richtingscoefficient ‘horizontaal’ delen door ‘verticaal’ in plaats van omgekeerd. Bij het berekenen van het verschil tussen 2 coordinaten waarbij 1 coordinaat negatief is een min vergeten.
A: (2- – 4)/(6-3) gedaan, dus horizontaal gedeeld door verticaal in plaats van omgekeerd
B: juist
C : (6-3)/(2-4) gedaan, dus verticaal gedeeld door horizontaal, maar min van ‘-4’ vergeten
D: (2-4)/(6-3) gedaan, dus horizontaal gedeeld door verticaal en min van ‘-4’ vergeten.
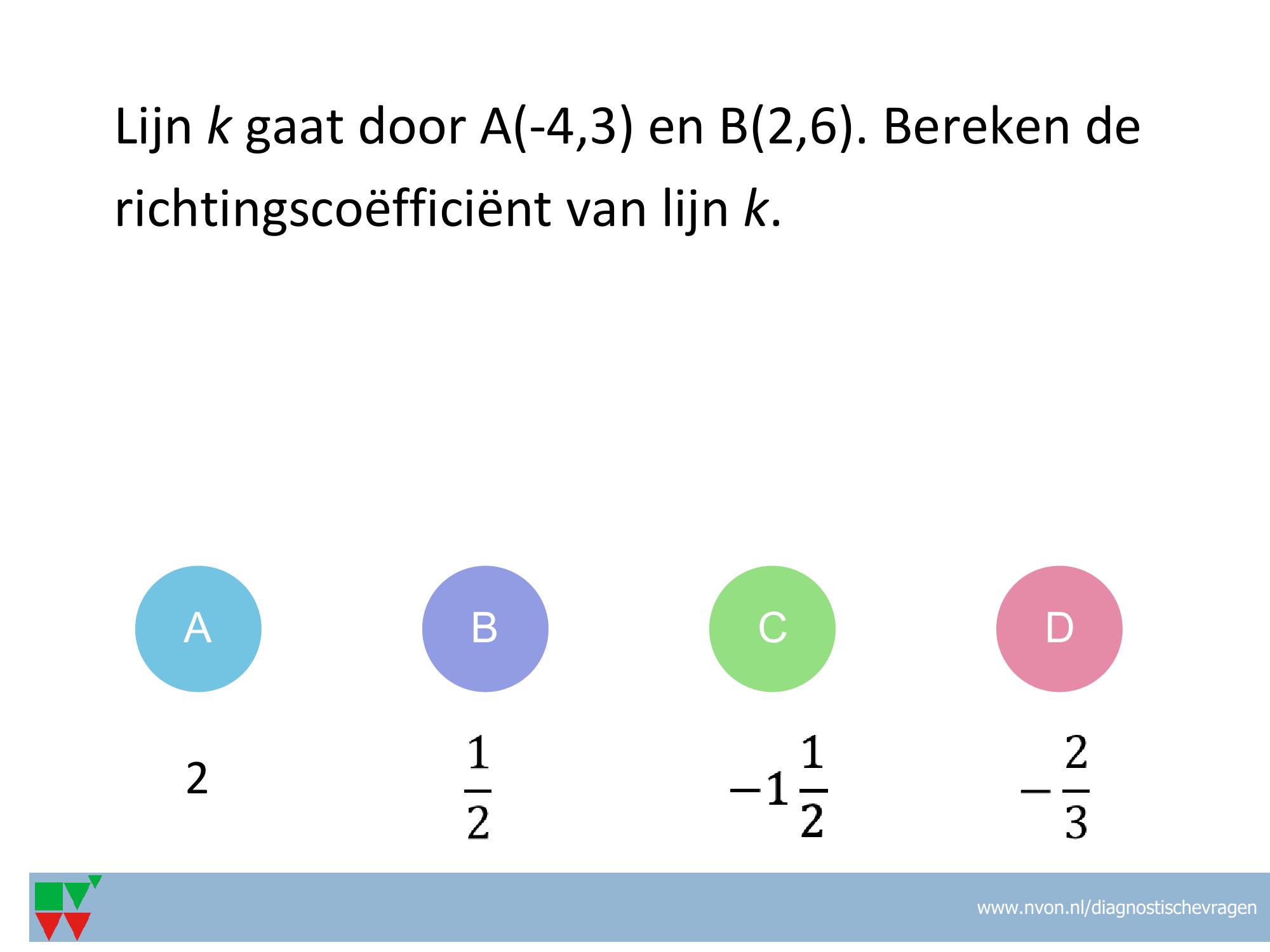
VF-49
Misvatting: Bij de richtingscoefficient ‘horizontaal’ delen door ‘verticaal’ in plaats van omgekeerd. Bij het berekenen van het verschil tussen 2 coordinaten waarbij 1 coordinaat negatief is een min vergeten.
A (-4- – 2)/(4-8) gedaan, dus horizontal/verticaal in plaats van omgekeerd
B: juist
C (-2-4)/(4-8) gedaan, horizontaal/verticaal en ook nog min vergeten in de teller
D (4-8)/(-2-4) gedaan, min vergeten in noemer
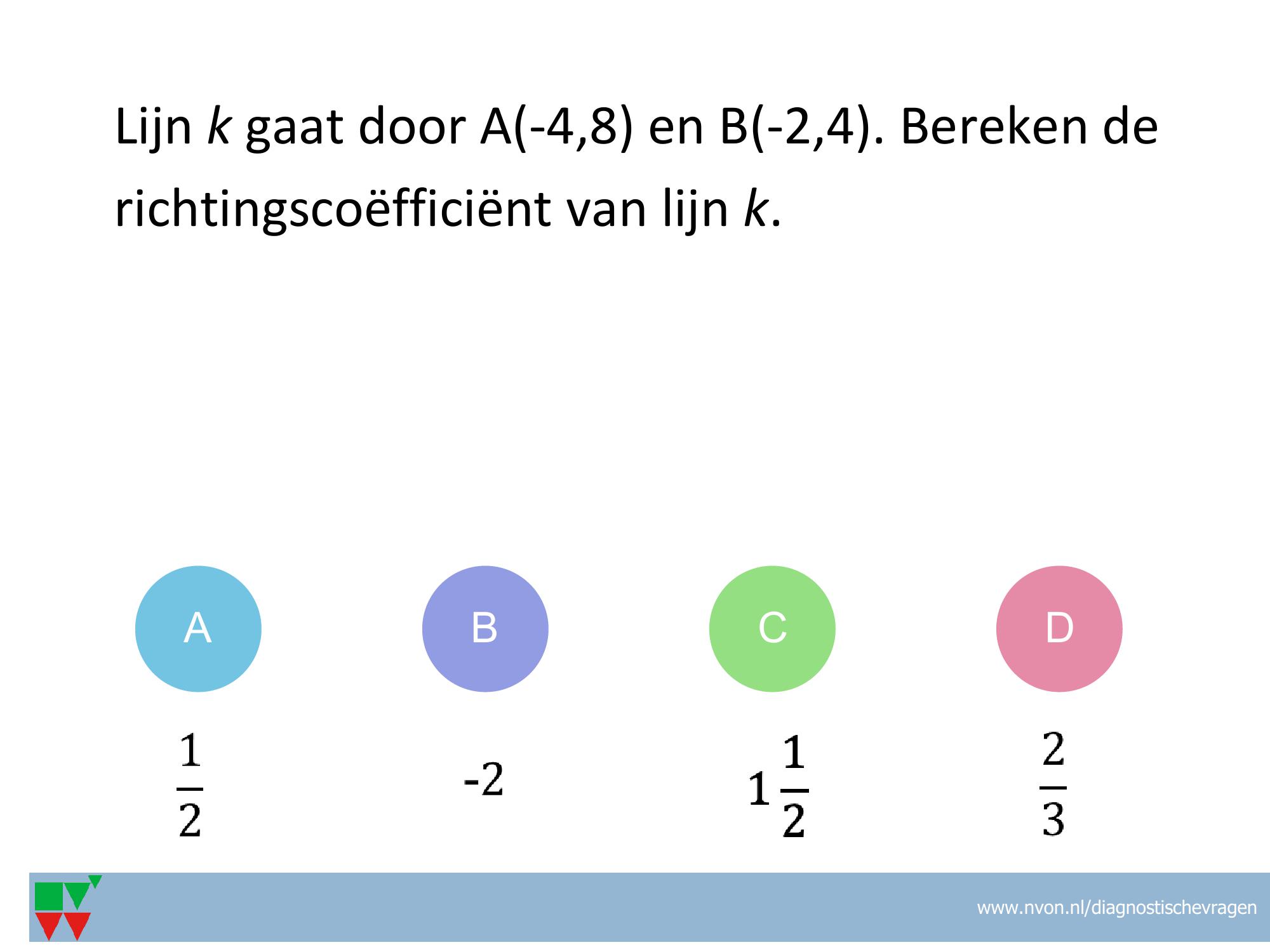
VF-50
Misvatting: Voor het berekenen van de rc niet naar de getallen op de assen kijken, maar het aantal hokjes tellen of horizontal/verticaal in plaats van andersom
A voor het berekenen van de rc zijn de hokjes geteld (wel verticaal/horizontaal)
B juist
C voor het berekenen van de rc hokjes geteld en horizontaal/verticaal in plaats van omgekeerd.
D voor het berekenen van de rc horizontaal/vertical in plaats van omgekeerd
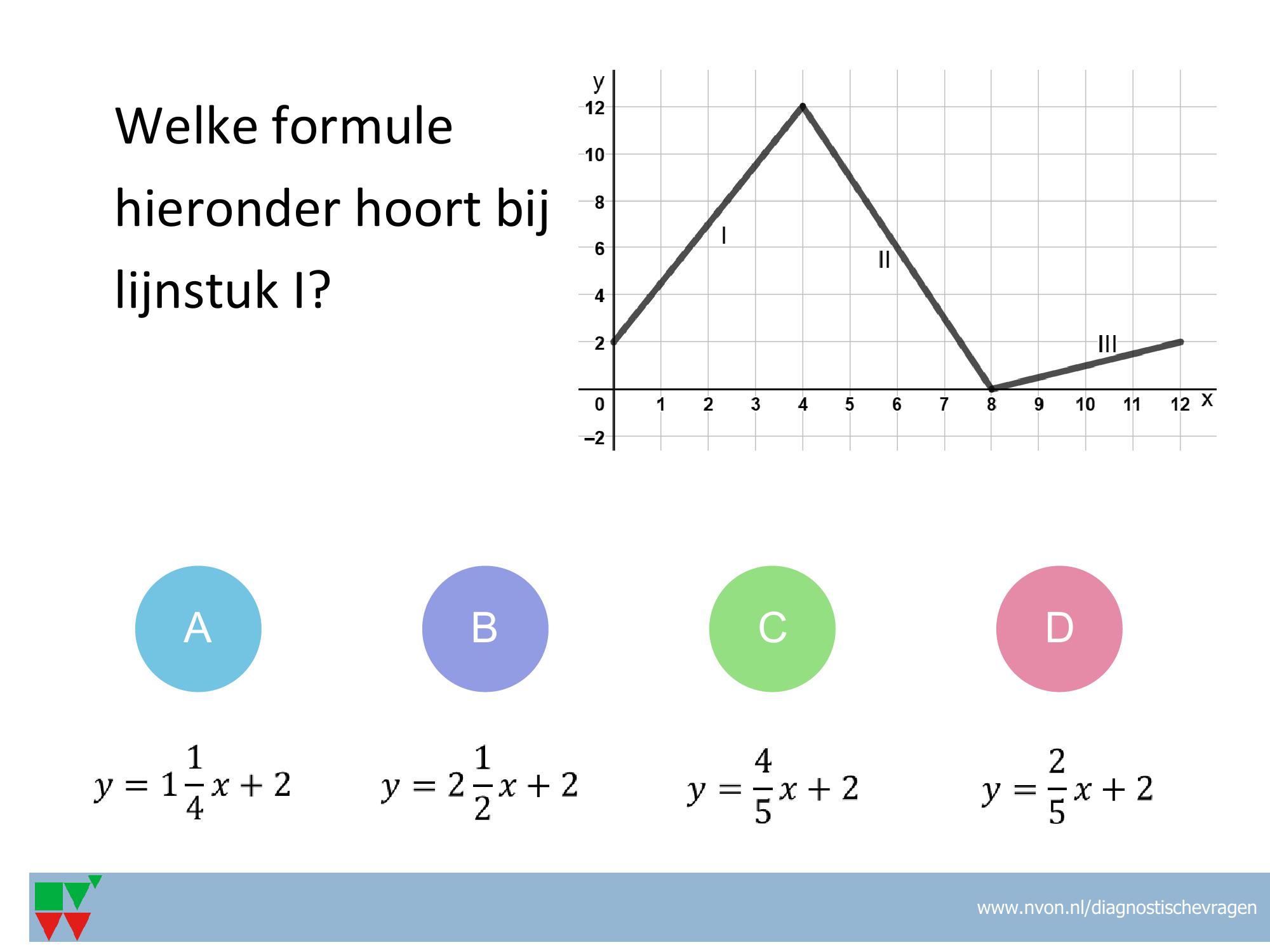
VF-51
Misvatting: min vergeten bij rc of ‘horizontaal gedeeld door verticaal’ in plaats van omgekeerd
A min vergeten bij rc (12-0)/(8-4) in plaats van (0-12)/(8-4)
B Juist
C ‘horizontaal gedeeld door verticaal’ en min vergeten
D ‘horizontal gedeeld door verticaal’
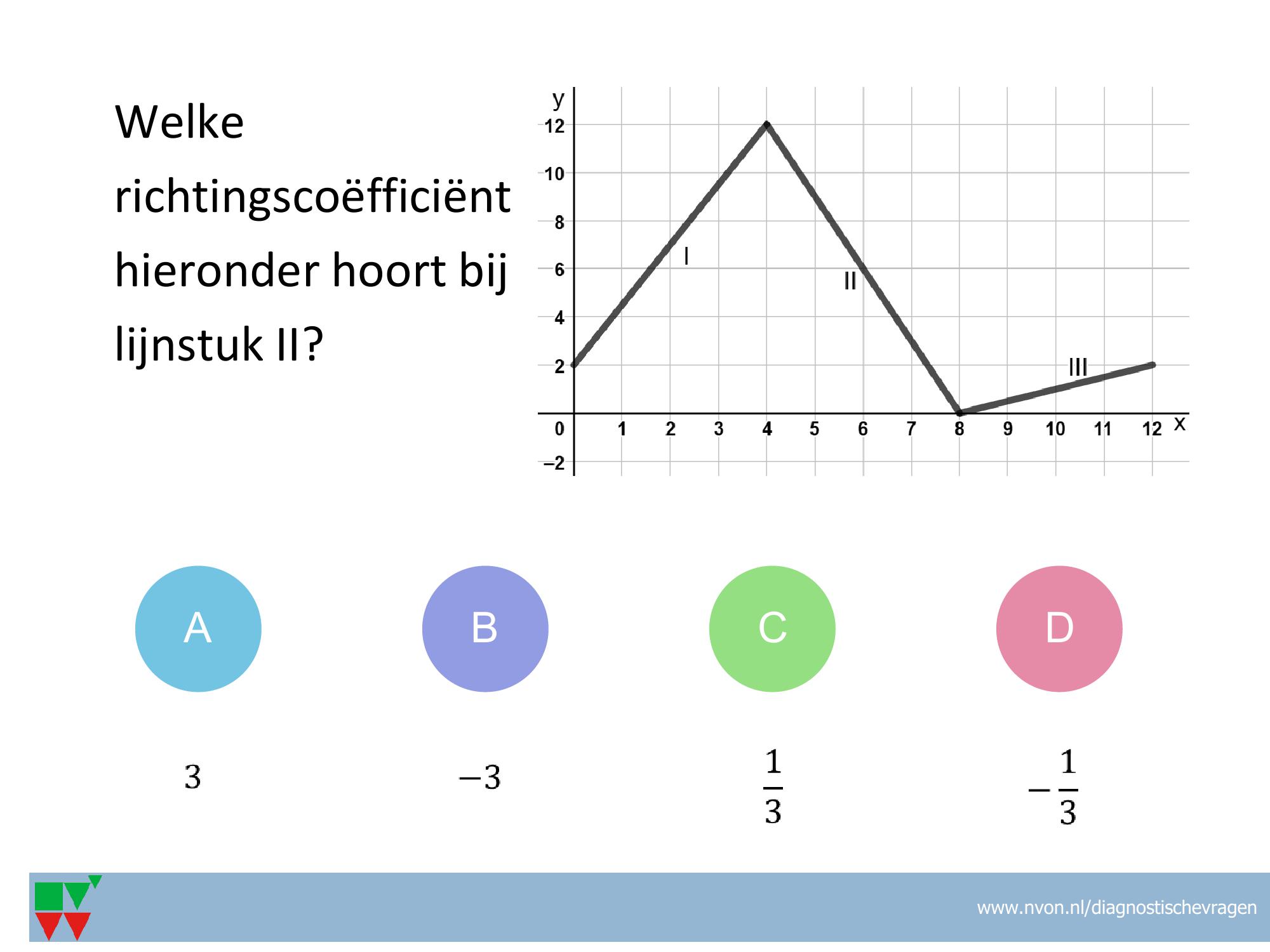
VF-52
Misvatting: min vergeten voor de rc (12-0 in plaats van 0-12) en bij begingetal gekeken bij welke y-coordinaat het lijnstuk begint in plaats van naar het snijpunt met de y-as
A min vergeten bij rc (12-0)/(8-4) in plaats van (0-12)/(8-4) en 12 genomen omdat het lijnstuk begint bij (4,12)
B rc is juist, bij begingetal 12 omdat het lijnstuk begint bij (4,12)
C min vergeten bij rc, begingetal is juist
D juist
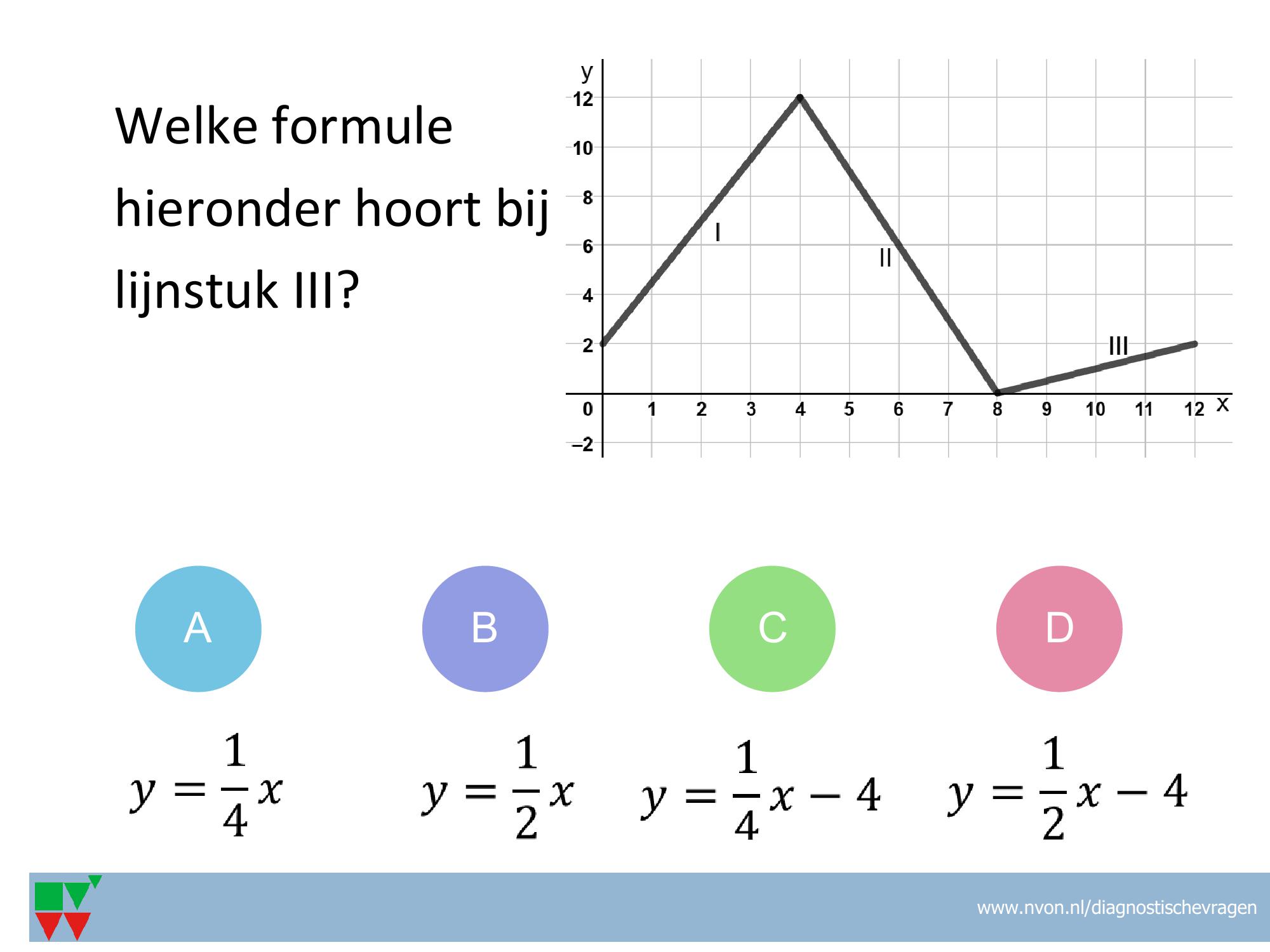
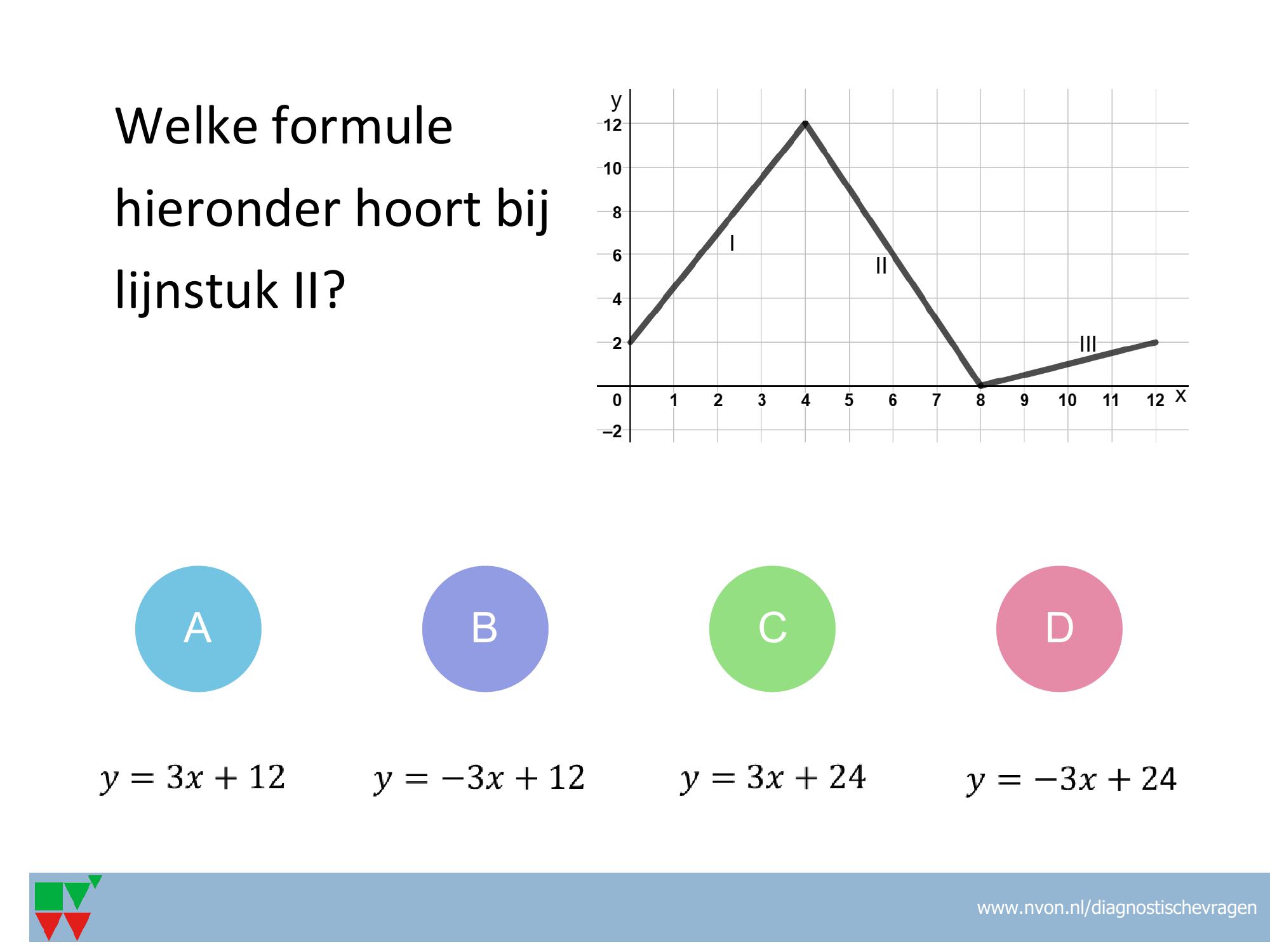
VF-53
Misvatting: Niet naar de getallen op de assen kijken, maar het aantal hokjes tellen en lijn niet doortrekken tot de y-as voor het bepalen van het begingetal
A: Voor richtingscoefficient wel verticaal/horizontaal maar naar aantal hokjes gekeken, begingetal 0 genomen omdat het lijnstuk op de x-as begint
B: Richtingscoefficient goed, maar als begingetal 0 genomen omdat het lijnstuk op de x-as begint
C: Bij richtingscoefficient hokjes geteld en niet naar de getallen op de assen gekeken.
D: Juist

De vragen en toelichtingen vallen onder een CC BY-SA 4.0 licentie https://creativecommons.org/licenses/by-sa/4.0